课堂引入就好像正餐前的开胃菜一样,开胃菜符合口味,后面正餐才有食欲。在课堂教学中一样,课堂引入是课堂教学的起始环节,也是课堂教学必须有的环节。课堂引入的好坏直接影响一节课的质量,一个有新颖、活力的引入就像一盘符合顾客口味的开胃菜,激发学生学习的欲望和兴趣。本文从教学经验和教学实例入手,对课堂教学引入进行分析和总结。

苏联著名教育实践家和教育理论家霍姆林斯基说过:“教学的起点,首先在于激发学生的兴趣和愿望”, 良好的开端是成功的一半。课堂引入是课堂教学的一个重要环节,是上好一堂课的关键。引入新课,就是通过各种方法引出所要讲述的课题,把学生领进本节课学习的大门,如果一堂课的开始老师引入生动、活泼,学生就兴趣盎然、精神集中的投入新课的学习当中,就会产生更好的效果。反之,老师上课一开始就提出新知识、新概念,会给学生以突兀感难以激发学生的兴趣。
任教几年以来,通过对我们学校一些老师听课发现,大部分老师的在平时上课中都是回归旧识引入或者直接引入,涉及到公开课很多老师的引入时间平均在两分钟到三分钟之间,但很多老师的引入起到实际效果的很少。有些老师,尤其是刚参加工作的年轻老师,只图表现气氛热烈,追求形式上的活泼,把学生的兴趣和注意力都引到看热闹上去,或过多的占用课堂教学时间,影响教学效果,结果偏离了主题,一堂课下来,热闹少不了,学生学习效果甚微。由此可以看出,教学中搞好课堂引入是很有必要的,好的课堂引入就像开胃菜一样,数量不在多,在于精,具有开胃的作用,能提高食欲。那么面对新教材如何提高学生的学习兴趣,怎样搞好课堂引入环节?新课有哪些引入方法,通过几年的教学实践,我总结的新课常用引入方法及案例如下:
一、 归纳引入法
归纳猜想是揭示科学规律的重要方法,也是数学引入新课常用的方法。
例1:二次根式的乘除法法则引入;
上课前两分钟,老师在黑板上板书:
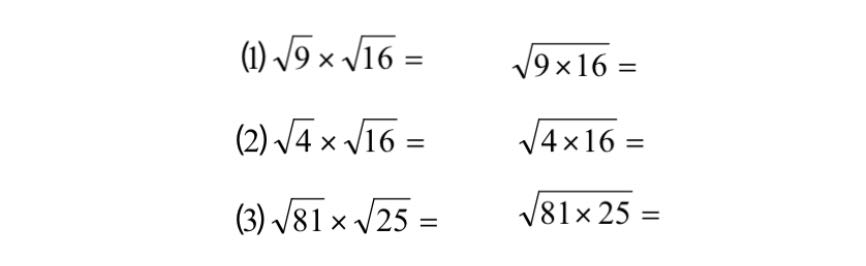
上课后,老师交代学生用3分钟时间在草稿本上计算三组结果。时间到后,找三个同学分别回答三组两个算式结果,然后提问“同学们发现了二次根式乘法的规律了嘛?”
有同学就发现了和的结果一样,同时下面两组的结果也一样。老师提问“你们能用字母表示我们二次根式乘法的法则嘛”从而得到二次根式乘法法则
例2:平方差公式引入
课前板书:
(1)(a+2)(a-2)= (2)(x+3)(x-3)=
(3)(-x+5)(x+5)= (4)(-y+5)(-y-5)=
上课后,老师叫同学自己利用前面的多项式乘多项式运算法则,计算出4个代数式的答案,分别叫4个同学回答4个答案。然后组织学生观察等式左边和右边的特点,有些学生可能发现不了,然后小组之间讨论一下,看能否总结出规律。然后在老师的引导下,发现了平方差的公式:
二、 复习引入法--------温故而知新
数学知识之间有着密切的联系,表现出极强的系统性。旧知识是新知识的基础,新知识又是旧知识的发展和延伸。学生学习数学知识的过程实质上是新知识与已有认知结构中的旧知识建立联系的过程。学生对与新知识联系最紧密的旧知识的理解掌握运用的程度,必然影响新知识的理解和掌握。这就要求老师在课堂引入时找准新旧知识的连接点,使学生感到新知识不新,激发学生的学习兴趣。这种方法在教学中常用。在学生已有知识为基础,通过提问、练习等教学活动,对相关的旧知识的进行回顾并掌握,从学过的知识过渡到即将要学的知识,从“已知的”拓展到“未知的”,既巩固了旧知识,又为新知识做了铺垫。
例:1:矩形的性质引入:
老师先提出:我们已经学习了平行四边形的概念,并在前面学习了平行四边形的性质,请大家回顾一下平行四边形的概念及性质。学生答后老师给出课题:很好!今天我们要学习一种特殊的平行四边形----矩形,它和前面学习的平行四边形有着非常密切的关系,请同学们在学习的过程中好好观察,思考,它和普通的平行四边形有何区别。
例2:二次根式的概念引入:
老师先提出:在初一我们学习实数里面学了平方根、算术平方根,请大家回顾一下平方根、算术平方根的定义及性质。学生回答后老师给出今天的课题:我们今天将在此基础上继续研究算术平方根即二次根式。
三、 故事、游戏引入法
华裔诺贝尔物理学奖获得者崔琦先生说过:“喜欢和好奇心比什么都重要”。根据学生的年龄特征和学生心理状态,结合数学的学科特点,引入的趣闻性是吸引学生(尤其是低年级学生)注意的关键。各种历史典故,名人轶事等在数学老师的精心组织和编排下,都可以成为沟通老师和学生之间感情交流的媒体,成为引用抽象数学问题的导线。讲点与新课有关的数学历史或故事或利用多媒体播放数学家的事迹,往往可引发学生浓厚的学习兴趣,甚至可给学生树立数学学习的榜样,增强探究精神和学习数学的毅力。
例1:在“勾股定理”的教学时,先以下面的数学故事引入:
毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形磁砖,但毕达哥拉斯不只是欣赏磁砖的美丽,而是想到它们和"数"之间的关系,于是拿了画笔并且蹲在地板上,选了一块磁砖以它的对角线AB为边画一个正方形,他发现这个正方形面积恰好等于两块磁砖的面积和。他很好奇,于是再以两块磁砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块磁砖的面积,也就是以两股为边作正方形面积之和。至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和。这个定理叫毕达哥拉斯定理,即我们本节课所学勾股定理。
例2,在学习平面直角坐标系第一节有序数对的时候我是这样引入的:
在今年中有一部非常火的谍战戏:《麻雀》,里面的陈深他们经常发电报,但是直接发文字被伪军截获一眼就看出了内容,怎么办?于是想到把电报加密,加密后接收方需要解密,解密需要密码本,以下表格为密码本:
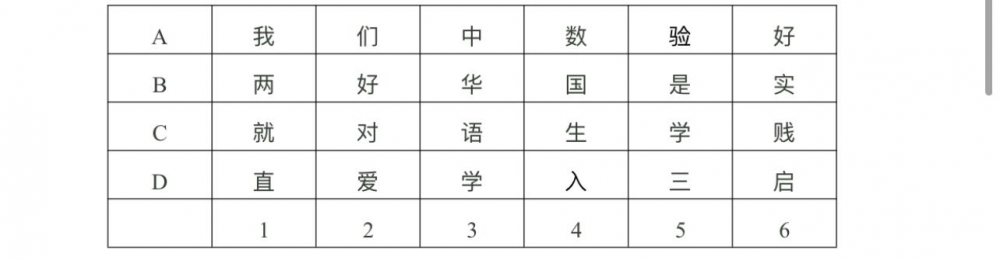
而接收方收到的电报内容是:A1,D2,A3,B4,同学们?陈深发的内容究竟是什么呢?
同学其回答:“我爱中国”
而老师继续提问,如果现在你是电视剧中的陈深,要发密电,电报内容为:“我是三好学生”,应该怎么发?
学生回答“A1,B5,D5,A6,C5,C4”或者” A1,B5,D5,A6,D5,C4 “
然后继续讨论同学们在教室座位编号:老师问,同学们,你们能不能说出自己的位置在?”有些同学就有点迷茫,问“老师,是从进门算第一排还是窗户算第一排?是排数在前还是列数在前?”
我回答它“哦,这是老师的疏忽,忘了说从哪里开始了,从进门第一排开始算第一排,排数在前,列数在后。所以我们应该规定顺序”从而引入今天的内容“有序数对”
例3:“常量和变量”一节
同学们都知道“乌鸦喝水这个故事”并播放乌鸦喝水这个故事的视频,然后提问“在乌鸦叼石头向水瓶中扔直到水瓶中的水到瓶口的位置的过程中,这里面哪些量变了,哪些量没变?”学生开始有些迷茫,然后老师引导,整个过程中水的体积变了嘛?学生马上反应过来一齐回答我不变,那水瓶中的石头数量变了没有了?学生马上回到石头的数量在变并且变多”然后老师提出今天的课题“这就是我们今天要探究的内容-常量和变量。”
四、 直接引入法------开门见山
开门见山的引入法是最基本最常见的一种引入方式,在上课一开始,老师就直接揭示课题,强调本节课的重难点,将相关学习内容直接呈现给学生,用最简洁的语言直接阐明对学生的要求,简洁明快地讲述或设问,引起学生的注意,使学生心中有数。诱发探求新知识的兴趣,把学生分散的注意力引导到课堂教学中来。这种方法要求老师语言精炼、简短、生动、明确,使学生产生一种紧迫感,激发学生的学习兴趣。
例1:“二次根式的加减”的引入:
老师说“我们已经学习了二次根式的定义,性质和乘除,本节课,我们将运用概念及法则来学习二次根式的加减运算“,直接抬出课题,了解了本节课的主要内容,明确了本节课的目标。
五、设疑引入入法
设疑引入法即所谓 “学起于思,思源于疑”,是教师通过设疑布置“问题陷阱”,学生在解答问题时不知不觉掉进“陷阱”,使他们的解答自相矛盾,引起学生积极思考,进而引出新课主题的方法。它的设计思路:教师提出问题,学生解答问题,针对学生出现的矛盾对立观点,引发学生的争论与思考,在激起学生对知识的强烈兴趣后,教师点题引入新课。
例1:在“函数的概念”的引入人
问题情境引入:阅读材料。回答问题。
一枚炮弹发射后。经过26s落到地面击中目标。炮弹的射高为845m.炮弹距地面的h随时间t变化的规律是h=130t一5t2。
(1)这个实例中的变量有哪些?
(2)它们之间的对应(依赖)关系是怎样表现的?
(3)填表(4)时间t的取值范围— — 。
(5)飞行高度h的取值范围— — 。
(6)设炮弹的飞行时间t的变化范围是数集A,炮弹距地面高度h的变化范围是数集B。对于 中的每一个时间t,按照对应关系,都有惟一确定值:距地面高度h,学生通过循序渐进的完成任务(过程与体验),有助于抽象出“函数概念”。这样的导人设计,让学生在思考中进入研究探索的状态。
在实际教学中,引入的类型和方法有很多,不只是以上几种。对不同的学科、不同的内容有不同的引入方法。即使是同一个内容也可以用不同的方法引入。引入的方法并不是孤立的,各种方法都在交叉使用。但这些都不是问题的关键,最重要的是引入的方式及引入的例子要贴近学生、贴近生活、贴近教学,吸引学生,激发学生的求知欲。在整个数学活动过程中,老师应想方设法设计好每节课的引入,使学生产生一种主动积极的态度,充分发挥学生非智力因素,让不同的学生都会在自己原有的水平上得到发展,都能体验到数学活动中创造的乐趣和成功的喜悦,树立起学好数学的信心,从而实现《新课程标准》提出的“人人学有价值的数学;人人都能获得必要的数学;不同人在数学上得到不同的发展。”

【免责声明】上游新闻客户端未标有“来源:上游新闻-重庆晨报”或“上游新闻LOGO、水印的文字、图片、音频视”等稿件均为转载稿。如转载稿涉及版权等问题,请联系上游。